What is Condition coverage?

This is closely related to decision coverage but has better sensitivity to the control flow. However, full condition coverage does not guarantee full decision coverage.

• Condition coverage reports the true or false outcome of each condition.
• Condition coverage measures the conditions independently of each other.

Other control-flow code-coverage measures include linear code sequence and jump (LCSAJ) coverage, multiple condition coverage (also known as condition combination coverage) and condition determination coverage (also known as multiple condition decision coverage or modified condition decision coverage, MCDC). This technique requires the coverage of all conditions that can affect or determine the decision outcome.

What is Branch Coverage or Decision Coverage? Its advantages and disadvantages

• Branch coverage is also known as Decision coverage or all-edges coverage.
• It covers both the true and false conditions unlikely the statement coverage.

• A branch is the outcome of a decision, so branch coverage simply measures which decision outcomes have been tested. This sounds great because it takes a more in-depth view of the source code than simple statement coverage
• A decision is an IF statement, a loop control statement (e.g. DO-WHILE or REPEAT-UNTIL), or a CASE statement, where there are two or more outcomes from the statement. With an IF statement, the exit can either be TRUE or FALSE, depending on the value of the logical condition that comes after IF.

Advantages of decision coverage:

• To validate that all the branches in the code are reached
• To ensure that no branches lead to any abnormality of the program’s operation
• It eliminate problems that occur with statement coverage testing

Disadvantages of decision coverage:

• This metric ignores branches within boolean expressions which occur due to short-circuit operators.

The decision coverage can be calculated as given below:

In the previous section we saw that just one test case was required to achieve 100% statement coverage. However, decision coverage requires each decision to have had both a True and False outcome. Therefore, to achieve 100% decision coverage, a second test case is necessary where A is less than or equal to B which ensures that the decision statement ‘IF A > B’ has a False outcome. So one test is sufficient for 100% statement coverage, but two tests are needed for 100% decision coverage. It is really very important to note that 100% decision coverage guarantees 100% statement coverage, but not the other way around.

1 READ A
2 READ B
3 C = A – 2 *B
4 IFC <0THEN
5 PRINT “C negative”
6 ENDIF
Code sample 4.3

Let’s suppose that we already have the following test, which gives us 100% statement coverage for code sample 4.3.

TEST SET 2   Test 2_1: A = 20, B = 15

The value of C is -10, so the condition  ‘C < 0’ is True, so we will print ‘C negative’ and we have executed the True outcome from that decision statement. But we have not executed the False outcome of the decision statement. What other test would we need to exercise the False outcome and to achieve 100% decision coverage?

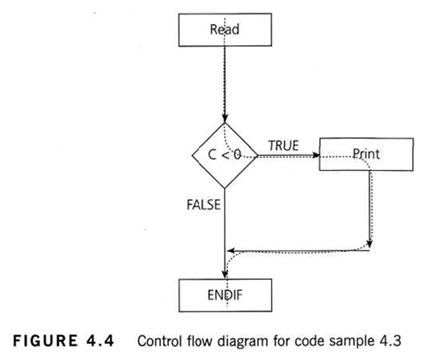
Before we answer that question, let’s have a look at another way to represent this code. Sometimes the decision structure is easier to see in a control flow diagram (see Figure 4.4).

The dotted line shows where Test 2_1 has gone and clearly shows that we haven’t yet had a test that takes the False exit from the IF statement.
Let’s modify our existing test set by adding another test:

TEST SET 2
Test 2_1: A = 20, B = 15
Test 2_2: A = 10, B = 2

This now covers both of the decision outcomes, True (with Test 2_1) and False (with Test 2_2). If we were to draw the path taken by Test 2_2, it would be a straight line from the read statement down the False exit and through the ENDIF. We could also have chosen other numbers to achieve either the True or False outcomes.